Algoritmo de Euclides

¿Que es el algoritmo de Euclides?

El algoritmo de Euclides es un procedimiento para calcular el máximo común divisor (m.c.d.) de dos números. 

Euclides fue un matemático griego que recopiló varios datos en una obra llamada Elementos. Esta obra es considerada como uno de los pillares de las matemáticas, y Euclides el "padre de la geometría". 

En Elementos, Euclides explica que el máximo común divisor de dos números se puede encontrar dividiendo el número mayor por el número menor. Si la división es exacta, el m.c.d. es el número menor. Si la división no es exacta, entonces se toma el residuo, y se divide tantas veces como haga falta para llegar a una división sin residuo. El m.c.d. es el último número por cuál se puede dividir. 

Aunque la palabra algoritmo nos hace pensar en cálculos complejos resueltos por ordenadores, en nuestro caso el cálculo es mucho más sencillo. Solo hace falta seguir los siguientes pasos.

Pasos del algoritmo de Euclides

1 Se divide el número mayor entre el menor.

2 Si la división es exacta, el divisor es el m.c.d.

3 Si la división no es exacta, dividimos el divisor entre el resto obtenido y continuamos de esta forma hasta obtener una división exacta. El m.c.d. es el último divisor.

Algoritmo original de Euclides

Ejemplo del algoritmo original de Euclides.

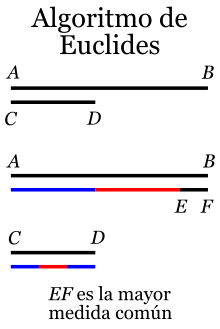
En la concepción griega de la matemática, los números se entendían como magnitudes geométricas. Un tema recurrente en la geometría griega es el de la conmensurabilidad de dos segmentos: dos segmentos (números) AB y CD son conmensurables cuando existe un tercer segmento PQ que cabe exactamente un número entero de veces en los primeros dos; es decir, PQ «mide» (mensura: medida) a los segmentos AB y CD.

No cualquier par de segmentos es conmensurable, como encontraron los pitagóricos cuando establecen que el lado y la diagonal de un cuadrado no son conmensurables, pero en el caso de dos segmentos conmensurables se desea hallar la mayor medida común posible.

Euclides describe en la proposición VI I.2 de sus Elementos un método que permite hallar la mayor medida común posible de dos números (segmentos) que no sean primos entre sí, aunque de acuerdo a la época tal método se explica en términos geométricos, lo que se ilustra en la siguiente transcripción.

Entender el algoritmo de Euclides Si examinamos el algoritmo de Euclides podemos ver que hace uso de las siguientes propiedades: MCD(A,0) = A. MCD(0,B) = B. Si A = B⋅Q + R y B≠0, entonces MCD(A,B) = MCD(B,R) , donde Q es un entero y R es un entero entre 0 y B-1. Las primeras dos propiedades nos permiten encontrar el MCD si cualquiera de los dos números es 0.    La tercera propiedad nos permite tomar un problema más grande y más  difícil de resolver, y reducirlo a un problema más pequeño y más fácil de resolver.   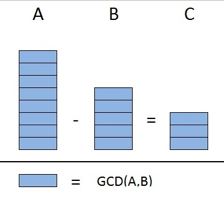El algoritmo de Euclides hace uso de estas propiedades al reducir rápidamente el problema  en problemas más y más fáciles, al usar la tercera propiedad, hasta que se resuelve fácilmente mediante el uso una de las primeras dos propiedades.   Podemos entender por qué funcionan estas propiedades al demostrarlas.   Podemos demostrar que MCD(A,0)=A como sigue: El entero más grande que puede dividir uniformemente a A es A. Todos los enteros dividen uniformemente a 0, puesto que para cualquier número entero, C, podemos escribir C ⋅ 0 = 0. Así que podemos concluir que A debe dividir uniformemente a 0. El número más grande que divide tanto a A como a 0 es A. La demostración para MCD(0, B)=B es similar. (Misma demostración, pero reemplazamos  A con B). Para demostrar que MCD(A,B)=MCD(B,R) lo primero que tenemos que mostrar es que MCD(A,B)=MCD(B,A-B). Supón que tenemos tres enteros A, B y C tales que A-B=C. Demostración de que MCD(A,B) divide uniformemente a C El MCD(A,B), por definición, divide uniformemente a A. Como resultado, A debe ser algún múltiplo de MCD(A,B). Es decir, X⋅MCD(A,B)=A, donde X es algún número entero. El MCD(A,B), por definición, divide uniformemente a B. Como resultado, B debe ser algún múltiplo de MCD(A,B). Es decir, Y⋅MCD(A,B)=B, donde Y es algún número entero. 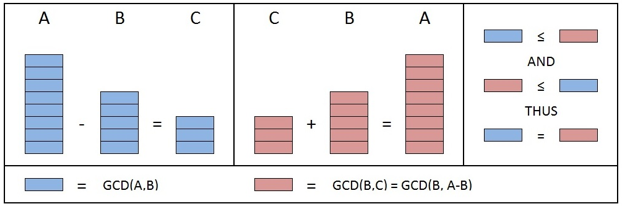A-B=C nos da: X⋅MCD(A,B) - Y⋅MCD(A,B) = C (X - Y)⋅MCD(A,B) = C Así que podemos ver que MCD(A,B) divide uniformemente a C. Una ilustración de esta demostración se muestra en la parte izquierda de la siguiente figura: Demostración de que MCD(B,C) divide uniformemente a A El MCD(B,C), por definición, divide uniformemente a B. Como resultado, B debe ser algún múltiplo de MCD(B,C). Es decir, M⋅MCD(B,C)=B, donde M es algún número entero. El MCD(B,C), por definición, divide uniformemente a C. Como resultado, C debe ser algún múltiplo de MCD(B,C). Es decir, N⋅MCD(B,C)=C, donde N es algún número entero. A-B=C nos da: B+C=A. 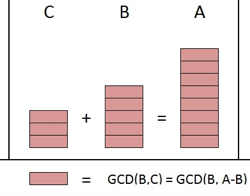M⋅MCD(B,C) + N⋅MCD(B,C) = A (M + N) ⋅ GCD(B,C) = A Así que podemos ver que MCD(B,C) divide uniformemente a A. Una ilustración de esta demostración se muestra en la siguiente figura: Demostración de que MCD(A,B)=MCD(A,A-B) MCD(A,B) por definición, divide uniformemente a B. Ya demostramos que MCD(A,B) divide uniformemente a C. Como el MCD(A,B) divide uniformemente tanto a B como a C, es un divisor común de B y de C. MCD(A,B) debe ser menor que o igual a MCD(B,C), porque MCD(B,C) es el “máximo” común divisor de B y de C. MCD(B,C) por definición, divide uniformemente a B. Ya demostramos que MCD(B,C) divide uniformemente a A. Como el MCD(B,C) divide uniformemente tanto a A como a B, es un divisor común de A y de B. MCD(B,C) debe ser menor que o igual a, MCD(A,B), porque MCD(A,B) es el “máximo”  común divisor de A y de B. Dado que MCD(A,B)≤MCD(B,C) y MCD(B,C)≤MCD(A,B) podemos concluir que: MCD(A,B)=MCD(B,C). Que es equivalente a: MCD(A,B)=MCD(B,A-B). Una ilustración de esta demostración se muestra en la parte derecha de la siguiente figura.     Demostración de que MCD(A,B) = MCD(B,R)   Ya demostramos que MCD(A,B)=MCD(B,A-B).   El orden de los términos no importa, así que podemos decir que MCD(A,B)=MCD(A-B,B).   Podemos aplicar repetidamente MCD(A,B)=MCD(A-B,B) para obtener:   MCD(A,B)=MCD(A-B,B)=MCD(A-2B,B)=MCD(A-3B,B)=...=MCD(A-Q⋅B,B).   Pero A= B⋅Q + R, así que A-Q⋅B=R.   Por lo tanto MCD(A,B)=MCD(R,B).   El orden de los términos no importa, así que:   MCD(A,B)=MCD(B,R).